Hyperledger Besu는 엔터프라이즈 환경에서 가장 광범위한 합의 알고리즘을 지원하는 이더리움 클라이언트로, 다양한 네트워크 요구사항에 맞춰 최적화된 합의 메커니즘을 제공합니다12. 이 분석에서는 Besu가 지원하는 5가지 주요 합의 알고리즘인 QBFT, IBFT 2.0, Clique, Ethash, Proof of Stake의 핵심 특징과 차이점을 상세히 살펴보겠습니다345.
Besu의 플러그인 합의 아키텍처
Hyperledger Besu는 모듈형 아키텍처를 기반으로 하여 다양한 합의 알고리즘을 플러그인 형태로 지원합니다5. 이러한 설계를 통해 개발자와 기업은 자신의 요구사항에 가장 적합한 합의 메커니즘을 선택할 수 있습니다67.
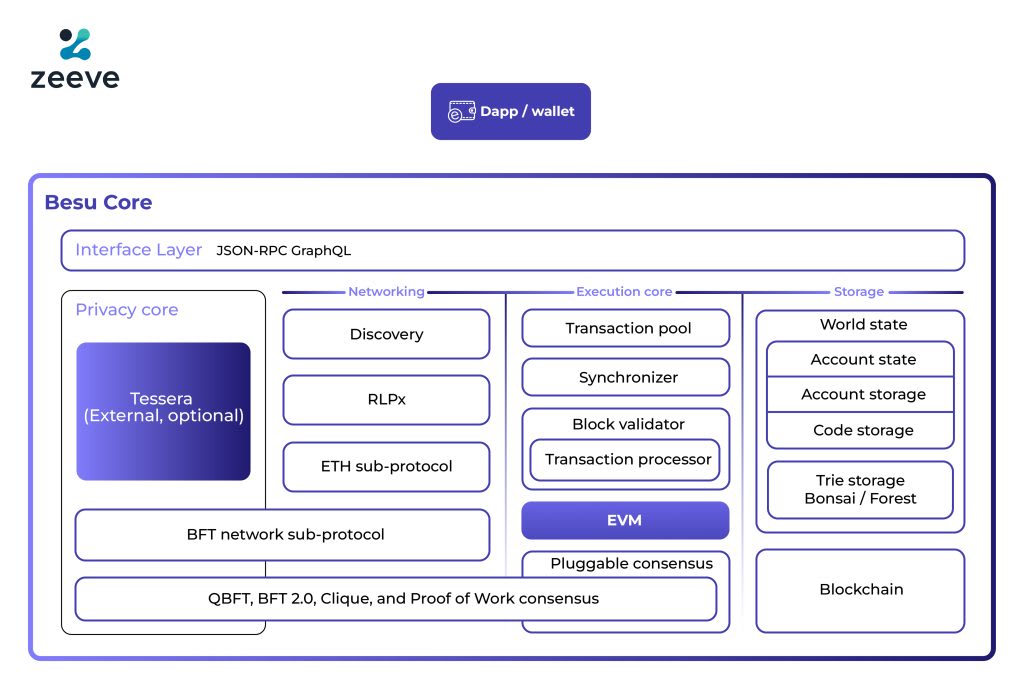
Hyperledger Besu core architecture illustrating pluggable consensus mechanisms including QBFT, BFT 2.0, Clique, and Proof of Work zeeve
권위 증명 (PoA) 합의 알고리즘
QBFT (Quorum Byzantine Fault Tolerance)
QBFT는 Besu에서 프라이빗 네트워크용으로 권장되는 최고급 엔터프라이즈 합의 프로토콜입니다35. 이 알고리즘은 승인된 검증자들이 트랜잭션과 블록을 검증하며, 검증자들이 차례대로 다음 블록을 생성합니다2.
QBFT의 핵심 특징으로는 즉시 최종성(immediate finality)을 보장하며, 최소 4개의 검증자가 필요합니다38. 네트워크가 정상적으로 작동하려면 전체 검증자의 2/3 이상이 생존해야 하므로, 최대 1/3의 검증자 실패를 허용합니다3.
성능 측면에서 QBFT는 약 166 TPS의 처리량을 달성할 수 있으며, 블록 생성 주기는 2초로 설정됩니다9. 이는 다른 PoA 알고리즘들보다 우수한 성능을 보여줍니다9.
IBFT 2.0 (Istanbul Byzantine Fault Tolerance 2.0)
IBFT 2.0은 기존 프라이빗 네트워크를 위해 지원되는 합의 알고리즘으로, IBFT 1.0의 안전성 문제를 해결하기 위해 개발되었습니다105. 이 프로토콜은 QBFT와 유사하게 즉시 최종성을 제공하며, 포크가 발생하지 않습니다311.
IBFT 2.0의 기술적 특징으로는 최소 4개의 검증자가 필요하며, 네트워크 운영을 위해 2/3 이상의 검증자가 활성화되어야 합니다23. 블록 생성 주기는 1-15초로 설정 가능하며, 일반적으로 5초가 기본값으로 사용됩니다1211.
성능 측면에서 IBFT 2.0은 약 100 TPS의 처리량을 보이며, QBFT보다는 상대적으로 느린 속도를 나타냅니다11. 그러나 안정적인 네트워크 운영과 즉시 최종성을 보장하는 장점이 있습니다10.
Clique
Clique는 Geth 클라이언트에서도 지원되는 PoA 알고리즘으로, 개발 및 테스트 환경에서 주로 사용됩니다123. 이 알고리즘은 다른 PoA 알고리즘들과 달리 즉시 최종성을 제공하지 않으며, 포크와 체인 재구성이 발생할 수 있습니다38.
Clique의 독특한 특징은 단일 검증자로도 운영이 가능하다는 점이며, 최대 절반의 검증자 실패를 허용하는 높은 내결함성을 제공합니다38. 이는 QBFT나 IBFT 2.0의 33% 내결함성보다 훨씬 관대한 수준입니다3.
성능 측면에서 Clique는 약 98 TPS의 처리량을 보이며, 블록 생성 주기는 15초로 설정됩니다1211. 상대적으로 빠른 처리 속도를 보이지만, 포크 발생 가능성으로 인해 프로덕션 환경에서는 권장되지 않습니다38.
작업 증명 (PoW) – Ethash
Ethash는 이더리움 메인넷에서 사용되던 전통적인 작업 증명 알고리즘으로, Besu에서는 소규모 개발 네트워크에서만 사용이 권장됩니다47. 이 알고리즘은 높은 계산 능력을 요구하며, 메모리 집약적인 특성을 가집니다6.
Ethash의 주요 특징으로는 완전한 분산화를 제공하며, 해시파워의 과반수 공격에 대한 저항성을 가집니다4. 그러나 극도로 낮은 성능(약 15 TPS)과 높은 에너지 소비로 인해 엔터프라이즈 환경에는 부적합합니다6.
지분 증명 (PoS) – Proof of Stake
Proof of Stake는 이더리움 메인넷과 퍼블릭 테스트넷에서 사용되는 합의 알고리즘으로, Besu는 합의 클라이언트와 함께 PoS 네트워크에 참여할 수 있습니다413. 이 알고리즘은 에너지 효율성과 확장성을 제공하며, 즉시 최종성을 보장합니다13.
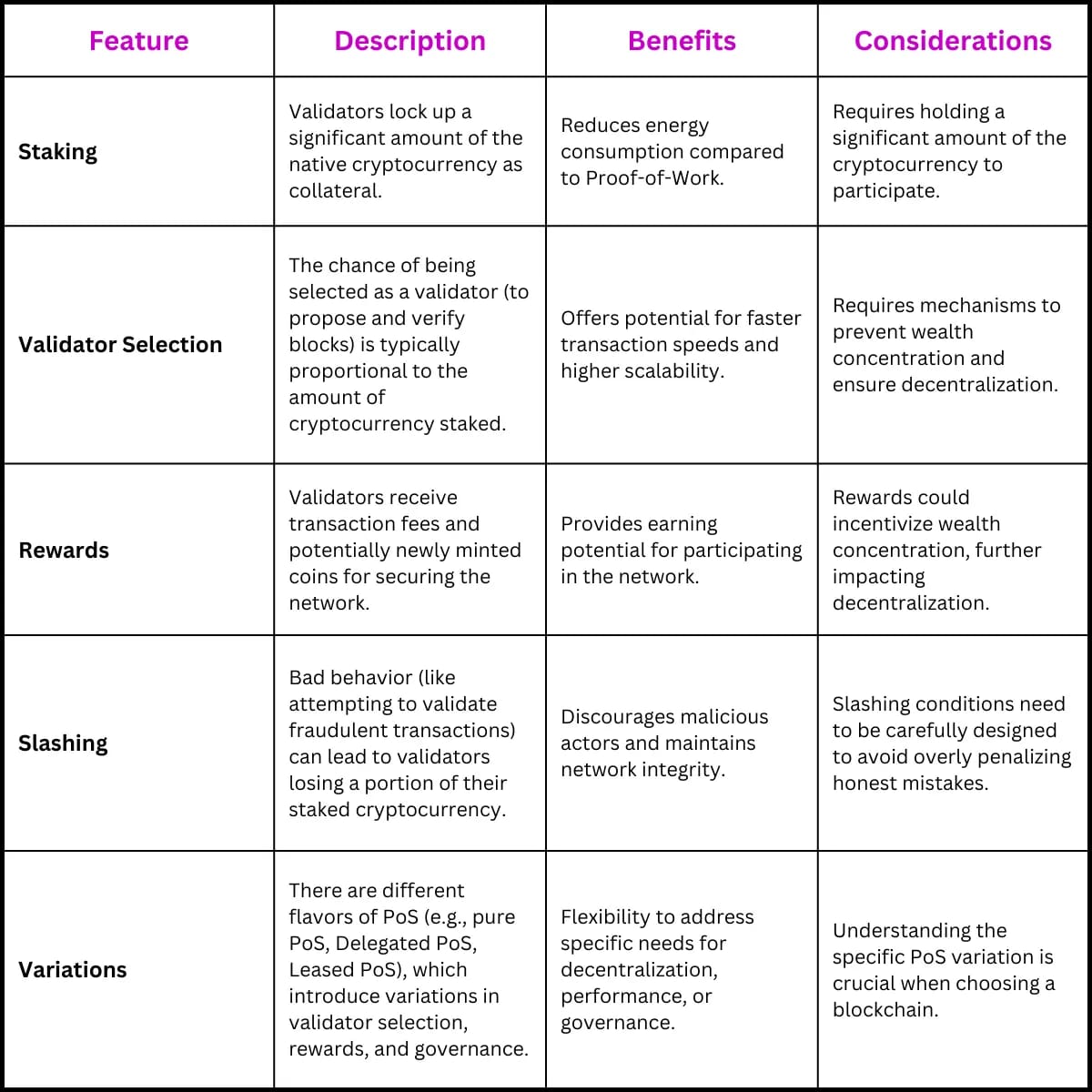
Table illustrating the features, descriptions, benefits, and considerations of the Proof-of-Stake (PoS) consensus mechanism tokenminds
PoS의 운영을 위해서는 별도의 합의 클라이언트가 필요하며, Engine API를 통해 실행 클라이언트인 Besu와 통신합니다13. 검증자가 되기 위해서는 일정량의 ETH를 스테이킹해야 하며, 악의적인 행동에 대해서는 슬래싱(slashing) 패널티가 적용됩니다13.
종합 성능 비교 분석
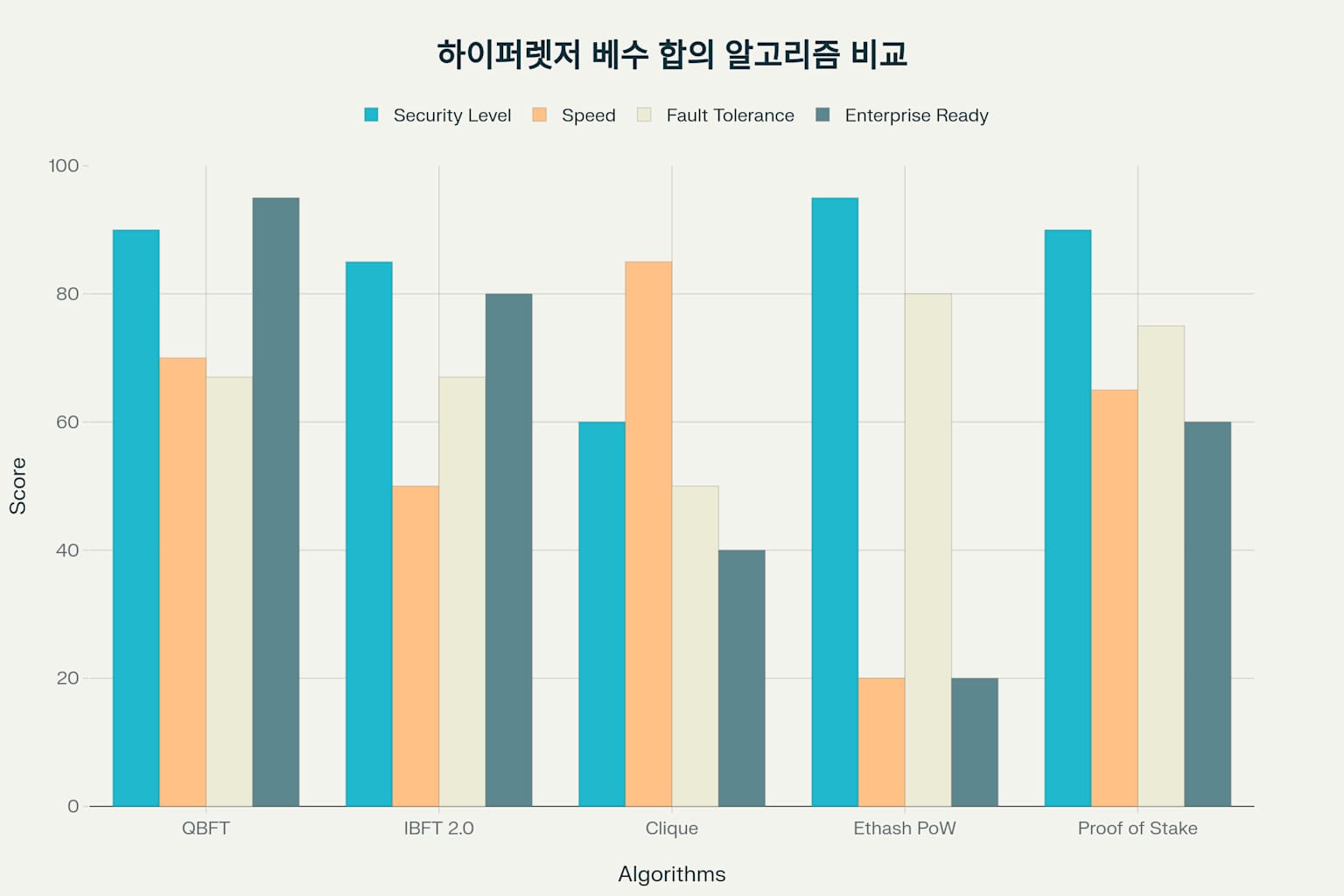
Hyperledger Besu 합의 알고리즘 종합 평가 비교
각 합의 알고리즘의 성능을 종합적으로 비교하면, QBFT가 엔터프라이즈 환경에서 가장 균형잡힌 성능을 제공합니다9. 처리량 측면에서 QBFT는 166 TPS로 가장 높은 성능을 보이며, IBFT 2.0은 100 TPS, Clique는 98 TPS를 기록합니다9.
블록 생성 시간에서는 QBFT가 2초로 가장 빠르며, 이는 실시간 트랜잭션 처리가 중요한 비즈니스 환경에서 큰 장점입니다9. 반면 Clique는 15초의 블록 시간을 가지며, 이는 검증자 수가 증가할수록 포크 확률이 높아지는 특성과 관련이 있습니다3.
내결함성 측면에서는 Clique가 50%의 검증자 실패를 허용하여 가장 관대한 반면, QBFT와 IBFT 2.0은 33%의 실패만을 허용합니다3. 이는 비잔틴 장애 허용 알고리즘의 이론적 한계에 기인합니다3.
besu-consensus-algorithms.md
생성된 파일
사용 사례별 권장사항
엔터프라이즈 프로덕션 환경
엔터프라이즈 프로덕션 환경에서는 QBFT가 최우선 선택으로 권장됩니다35. 이는 기업급 보안 수준, 빠른 블록 생성, 그리고 네트워크 분할에 대한 저항성을 제공하기 때문입니다5. 금융 서비스나 공급망 관리와 같이 높은 신뢰성이 요구되는 분야에서 특히 적합합니다2.
기존 IBFT 2.0 네트워크를 운영 중인 기업들은 안정성을 위해 현재 설정을 유지하는 것이 권장되지만, 새로운 네트워크 구축 시에는 QBFT로의 전환을 고려해야 합니다5.
개발 및 테스트 환경
개발 및 테스트 환경에서는 Clique가 적합한 선택입니다38. 단일 검증자로도 운영 가능하며, 빠른 개발 사이클을 지원합니다8. 또한 Geth와의 호환성으로 인해 다양한 이더리움 개발 도구와 원활하게 통합됩니다12.
메인넷 호환성 테스트가 필요한 경우에는 Ethash를 사용할 수 있지만, 낮은 성능과 높은 리소스 요구사항을 고려해야 합니다4.
퍼블릭 네트워크 참여
이더리움 메인넷이나 퍼블릭 테스트넷에 참여하려는 경우에는 Proof of Stake를 사용해야 합니다13. 이는 별도의 합의 클라이언트 설정과 ETH 스테이킹이 필요하지만, 이더리움 생태계와의 완전한 호환성을 제공합니다13.
결론
Hyperledger Besu는 다양한 합의 알고리즘을 지원함으로써 광범위한 블록체인 사용 사례에 대응할 수 있는 유연성을 제공합니다114. QBFT는 엔터프라이즈 환경에서 최고의 성능과 보안을 제공하며, IBFT 2.0은 기존 네트워크의 안정적인 운영을 지원합니다35. Clique는 개발 환경에서의 편의성을 제공하고, Proof of Stake는 퍼블릭 네트워크와의 호환성을 보장합니다313.
각 합의 알고리즘의 특성을 이해하고 프로젝트의 요구사항에 맞는 적절한 선택을 하는 것이 성공적인 블록체인 구현의 핵심입니다6. 특히 보안, 성능, 내결함성, 그리고 운영 복잡성을 종합적으로 고려하여 최적의 합의 메커니즘을 선택해야 합니다8.
- https://blog.naver.com/mage7th/222449548571
- https://velog.io/@hhoonjjang/Hyperledger-Besu-%EB%9E%80
- https://besu.hyperledger.org/24.5.2/private-networks/concepts/poa
- https://besu.hyperledger.org/private-networks/how-to/configure/consensus
- https://lf-hyperledger.atlassian.net/wiki/spaces/BESU
- https://fastercapital.com/ko/content/Hyperledger-Besu–%EA%B8%B0%EC%97%85%EC%97%90%EC%84%9C-%EC%9D%B4%EB%8D%94%EB%A6%AC%EC%9B%80%EC%9D%98-%EC%9E%A0%EC%9E%AC%EB%A0%A5-%EB%B0%9C%ED%9C%98.html
- https://consensys.io/blog/hyperledger-besu-understanding-proof-of-authority-via-clique-and-ibft-2-0-private-networks-part-1
- https://docs.catalyst.intellecteu.com/besu/Consensus%20Protocols/choose-a-cp.html
- https://core.ac.uk/download/639217432.pdf
- https://blog.naver.com/pcmola/222090486807
- https://joycecoder.tistory.com/entry/%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-Hyperledger
- https://joycecoder.tistory.com/117
- https://besu.hyperledger.org/public-networks/concepts/node-clients
- https://blog.web3labs.com/a-comparison-of-ethereum-clients
- https://www.kaleido.io/blockchain-blog/consensus-algorithms-poa-ibft-or-raft
- https://hsmang.tistory.com/18
- https://www.kaleido.io/blockchain-blog/comparing-hyperledger-fabric-and-hyperledger-besu
- https://entethalliance-japan.org/pdf/scaling8/8-5%E3%80%90NTT-TX%E3%80%91Performance_Assessment_of_Besu_with_Hyperledger_Caliper.pdf
- https://www.lfdecentralizedtrust.org/blog/2020/08/06/hyperledger-besu-1-5-performance-enhancements
- https://fastercapital.com/ko/content/Hyperledger–%EA%B8%80%EB%A1%9C%EB%B2%8C-%EC%B1%84%ED%83%9D%EC%9D%84-%EC%9C%84%ED%95%9C-%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-%EB%84%A4%ED%8A%B8%EC%9B%8C%ED%81%AC-%ED%99%95%EC%9E%A5.html
- https://jinnnkcoding.tistory.com/230
- https://hhlab.tistory.com/186
- https://www.slideshare.net/slideshow/hyperledger-besu-private-networks/269823250
- https://blockchain.kisa.or.kr/file/2024_%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8_%EC%86%94%EB%A3%A8%EC%85%98_%ED%8E%B8%EB%9E%8C.pdf
- https://developer.luniverse.io/docs/hyperledger-besu-sidechain
- https://jinnnkcoding.tistory.com/233